線形回帰 -入門 Kaggle House Pricesで試してみる-
目次
回帰(Regression)とは
教師あり学習には回帰と分類があります。
回帰は出力が連続値、分類は離散値という違いがあります。
線形回帰(Linear Regression)とは
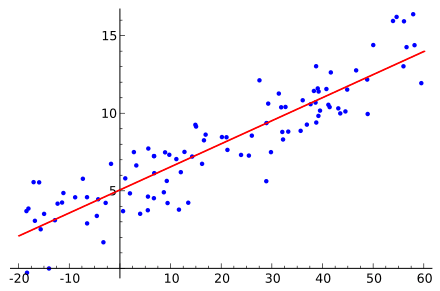
線形回帰とは下の画像のように、与えられたデータからそれを表現するもっともらしい式を導き出す回帰の一種です。
特に線形でざっくりと表現するものを指します。
In statistics, linear regression is a linear approach for modelling the relationship between a scalar dependent variable y and one or more explanatory variables (or independent variables) denoted X.
線形回帰の強みと弱み
強み
- 理解が簡単
弱み
- 線形にフィットしないような関数には弱い
簡単な関数を学習させてみる
簡単な関数を学習させる過程で線形回帰の実装法をさらいます。
h(x)の定義
m * nのデータXとn * 1のθに関して、
Xのあるデータx(一つの行)に関して以下のようにh(x)を定義します。
h(x) = θ0 * x0 + θ1 * x1 + ... + θn * xn
この関数のことをcouseraではHypothesis functionと呼んでいましたが、日本語訳が見つからなかったので、単にh(x)と呼びます。
これが予測によって出されたyの値になります。
当然初めはθは全てが0のベクトルなので、予測されたyの値も0になってしまいます。
ここから以下の損失関数を用いてどれくらい離れているかを算出し、θを更新していくことでもっともらしいθの値を導き出します。
上記ではXのうちの1行を使いました。まとめて全てを計算するには行列の計算を行います。
h(X) = X * θ
これでm * nのXとn * 1のθの積によりm * 1の予測結果が算出されます。
同じくm * 1のyと一致しているので計算がしやすくなります。
コードにすると以下のようになります。
def hypothesis_func(theta, X):
return np.dot(X, theta)
損失関数(Cost Function)J(θ)の定義
θを更新するにあたって、現在のθの値がどれくらい適切にyを予測することに役立つかの指標が必要になります。
それを損失関数と呼び、ここでは以下のように定義します(下の式ではθが0、1しかありませんが)。
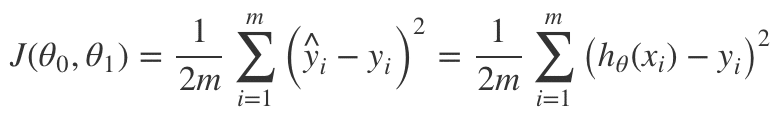
この値が0に近ければ近いほどもっともらしいθの値であると言えます。
最急降下法(Gradient Descent)によるθの更新
今回はこのJ(θ)を用いて最急降下法によりθを更新します。
式にすると以下の通りです(αは学習率といって別途設定します)。
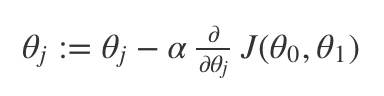
概念的に説明すると、θをそれぞれ最もJ(θ)が小さくなるように更新することになります。
上式の偏微分の項が傾きを現しています。これに対して学習率αで重み付けしてθを更新していきます。
さらに上式は以下のように変形することができます。
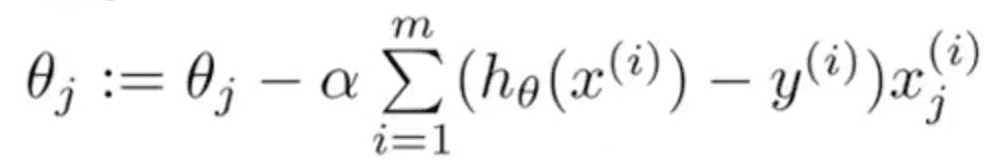
ベクトルで表現するとこんな感じ。
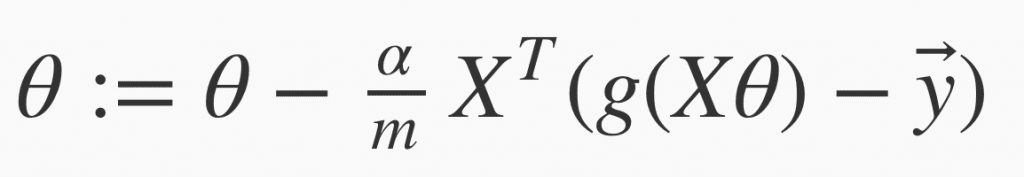
コードにすると以下のようになります。
def gradient_dechent(theta, X, y, alpha=0.01, iter_num=1000):
m = len(y)
for _ in range(iter_num):
dif = np.dot(X, theta) - y
dot = np.dot(dif.T, X).T
theta = theta - (alpha / m) * dot
return theta
試してみる
では適当なデータセットを用意して学習させてみます。
まずはこんな感じの3点のデータにフィットする直線を導きだしてみます。
答えは以下の通りですが、果たして学習できるでしょうか?
y = 0.5 + 0.5 * x
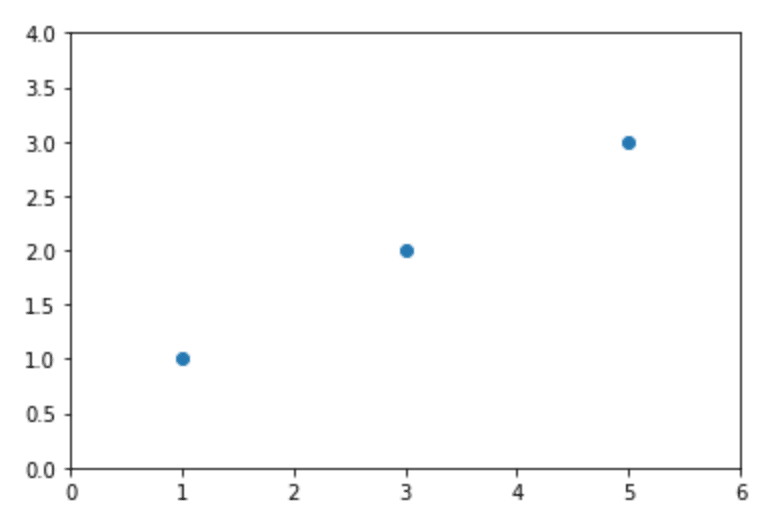
こんな感じ。

学習率0.03で1000回まわしてみたところ、theta[0] = 0.49945153, theta[1] = 0.50014367となったので、導きだした計算式はこちら。
y = 0.49945153 + 0.50014367 * x
まずまずですね。
さらにイテレーションを3000回に増やしたら0.5、0.5になるまで学習してくれました。
とりあえず線形回帰の流れはわかりました。
Kaggle House Pricesで試してみる
次にKaggleのHouse Pricesのデータで試しみます。
敷地面積や地域から住宅の価格を予測してみます。
まずはKaggle House Pricesのデータセットをダウンロードします(test.csvとtrain.csv)。
train.csvをpandasのread_csv()でチェックしてみます。
1460行81列のデータでした。
MSSubClassとかMSZoningとか馴染みのない単語ですね。おそらく住宅の何らかの要素を示しているのでしょうが。
今回はわかりやすく数値の属性だけを学習に使います。
最終的に求める出力の売り値と合わせて以下の8項目を取得しました。
MSSubClass: 建物の等級 LotFrontage: 間口の広さ LotArea: 敷地面積 PoolArea: プールの面積 MiscVal: その他雑多なものの価値 MoSold: 売れた月 YrSold: 売れた年 SalePrice: 売り値
これらを説明変数Xと目的変数yに分けます。
まずはLotArea(敷地面積)だけを使って予測してみましょう。
求めるべきSalePriceをyに、LotAreaをXに振り分けます。
house_data = house_data[['MSSubClass', 'LotFrontage', 'LotArea', 'PoolArea', 'MiscVal', 'MoSold', 'YrSold', 'SalePrice']].dropna() house_X = house_data[['LotArea']] house_y = house_data[['SalePrice']]
dropna()で欠損値がある行を除外しているのでいくらかデータが減り、
house_Xは12017、house_yは12011になりました。

さらにXには一列目にx0として1を挿入します。
x0 = np.ones([house_X.shape[0], 1]) house_X = np.concatenate((x0, house_X), axis=1)
これでhouse_Xは1201 * 2になりました。
次に初期のthetaも用意します。今回house_Xは2列なので、thetaは2 * 1になります。
theta = np.zeros([house_X.shape[1], 1])
学習させてみる
簡単な直線の時と同じように学習率0.03で1000回まわしてみたところ、
損失関数がどんどん増加してうまく学習できませんでした。
学習率を0.0000000001に変更したところ、
θ0 = 6.50823731e-03、θ1 = 1.23908709e+01となりました。
学習の様子(損失関数の減少の様子)はこんな感じ。
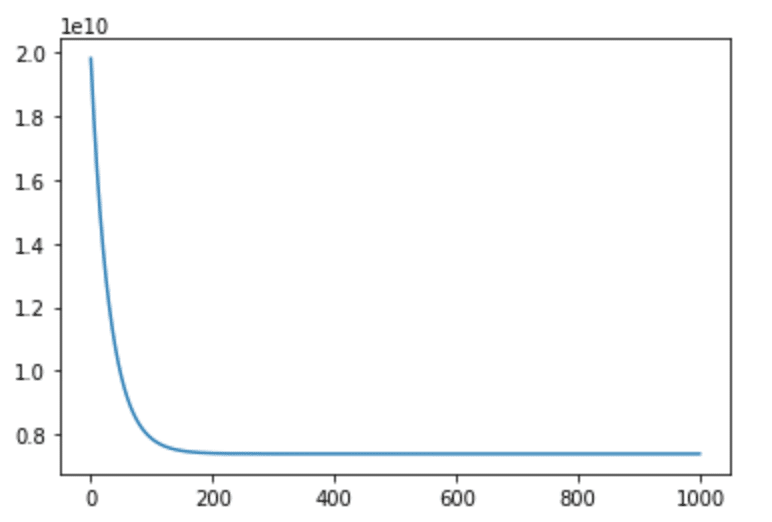
どうやら途中でプラトーに達してしまい、200回目以降は有効なθの更新が行われていないことがわかりました。
今回導きだしたθを用いて売り値を予測してみましょう。
house_dataの始めの5つほどを使ってみます。
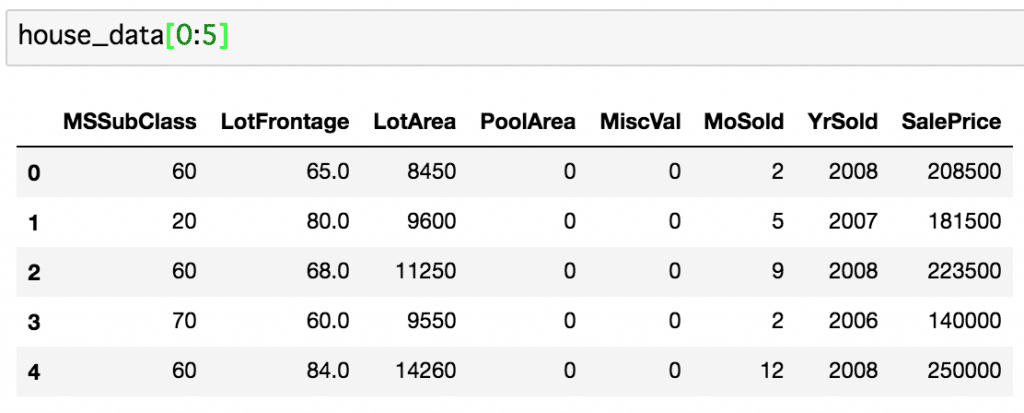
それぞれについて導出したθを使って売り値を予測してみます。
真の値と比較したのが下の画像の赤枠内です。
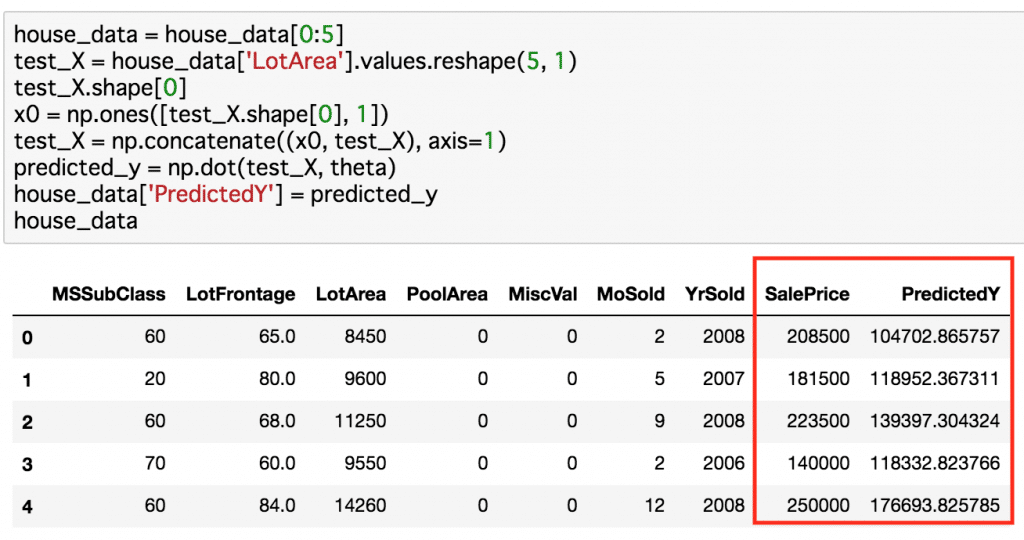
うーん、しょっぱい。
やはり面積だけでは決まらないようですね。
色々試してみる
以下の4つを使ってみました。
等級(MSSubClass)はぱっと見では今一影響がわかりませんでした。
高いのがいいのか低いのがいいのか。
LotFrontage: 間口の広さ LotArea: 敷地面積 PoolArea: プールの面積 MiscVal: その他雑多なものの価値
ファーストトライとしては悪くない?大まかな大小関係はなんとなーく取れてそうです。
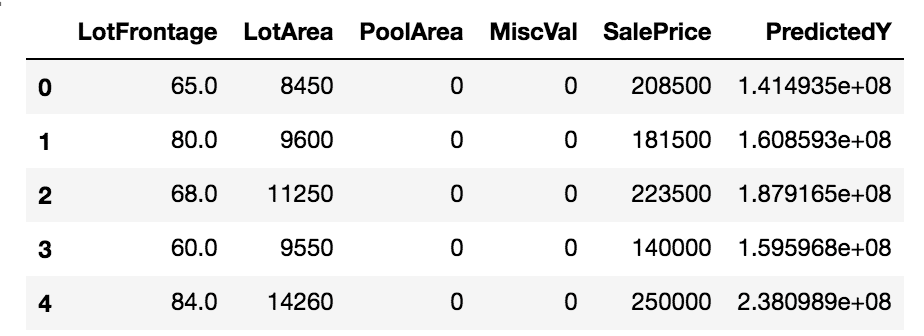
とりあえずこれで提出。
Score(小さい方が良い)は0.40243で順位は3727/3904でした。
![]()
線形回帰でどこまで上を目指せるのかはわかりませんが、まだまだ上は目指せるはずなので他のアルゴリズムを試して1周した頃に線形回帰での洗練化を行いたいと思います。
Kaggle House Pricesで上を目指す
他のアルゴリズムを一通り勉強したらここに戻ってきて、より良い結果が出せるように工夫してみます。
他のアルゴリズム
http://roy29fuku.com/human-animal-machine/machine/machine-learning/
参考
動画: coursera Machine Learning講座
courseraはスタンフォード大学などの授業をオンラインで無料受講できるMOOCです。
こちらのMachine Learning講座は非常に評価が高く、機械学習の入門として挙げる方が多いです。
無料という点では気軽に始められますが、それなりの英語力が要求される点で少し敷居が高いかもしれません(字幕はだいたい日本語が付いています)。
またお金を払えば正式にスタンフォード大学の修了証を取得できます。
書籍: ゼロから作るDeep Learning
学びの深い一冊です。ディープラーニングの中身を細かく解剖し、一つずつ自分で構築します。
Tensorflowなどのライブラリを使わないので、これらのライブラリの中身がどうなっているかということも学べます。
機械学習をブラックボックスではなくしっかり理解したい人向けです。